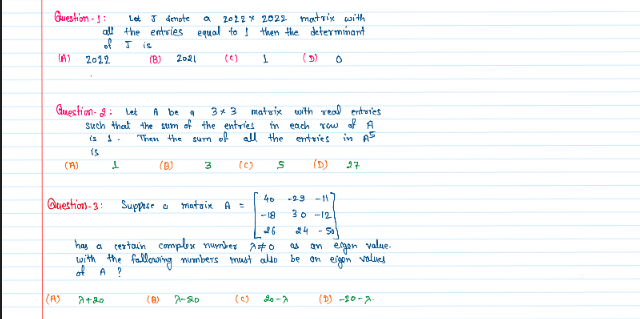
Engineering Mathematics handwritten notes pdf
Hello friends,
Engineering Mathematics handwritten notes pdf:- Today we are sharing the Engineering Mathematics handwritten notes pdf | Mathematics Handwritten Notes for you. These Engineering Mathematics handwritten notes pdf can prove to be important for the preparation of upcoming government exams like GATE, SSC CGL, BANK, RAILWAYS, RRB NTPC, LIC AAO, and many other exams. Engineering Mathematics handwritten notes pdf Download are very important for any Sarkari exam.
pdfdownload.in is an online educational website, where we are sharing Complete Engineering Mathematics handwritten notes pdf DOWNLOAD for GATE, UPSC, SSC, BANK, RAILWAY, LIC, and many other exams. This Math Handwriting Notes PDF 2022 Free Download in Hindi is very simple and easy to understand. We also cover basic subjects like Mathematics, Geography, History, General Science, Politics, etc. We also share study material including previous year’s question papers, current affairs, important sources, etc. for upcoming government exams. Our Engineering Mathematics handwritten notes pdf will help you prepare for any SARKARI EXAM.
Engineering Mathematics handwritten notes pdf For All Competitive Exams covered thoroughly under the guidance of subject experts. This Engineering Mathematics handwritten notes pdf mainly targeting RRB JE, RRB NTPC, SSC CGL & SSC CHSL. Engineering Mathematics handwritten notes pdf For All Competitive Exams !! Download all types of PDF related to Mathematics from here, we have provided direct link of notes here! Which you can download by clicking on the download link given below! If you have any kind of problem then you can write us in the comment box given below. We will assist you ASAP! We would be happy to assist you!
Download math Notes PDF
- Rakesh Yadav Advance Math book PDF Download
- Quicker Maths Book in Hindi PDF Download
- Rakesh Yadav Advance Math Book PDF in Hindi
- Abhinay Sir Maths Class Notes and Book Pdf
- Rakesh Yadav Math Class Notes Maths PDF in Hindi
- Math Trick in Hindi Notes PDF Download
- Disha Maths Book For SSC PDF Download
- maths books for competitive exams pdf free download
- Math Short Tricks Notes PDF in Hindi Download
- Math formula in hindi pdf for Competitive exams
Most Important Engineering Mathematics Question
Q 1. Two men on a surface want to meet each other. They have taken the point (0, 0) as meeting point. The surface is 3-D and its equation is f(x,y) = x−234y9x+(y)43. Given that they both play this game infinite number of times with their starting point as (908, 908) and (90, 180)
(choosing a different path every time they play the game). Will they always meet?
a) They will not meet every time
b) They will meet every time
c) Insufficient information
d) They meet with probability 1⁄2
Answer: a
Explanation: The question is asking us to simply find the limit of the given function exists as the pair (x, y) tends to (0, 0) (The two men meet along different paths taken or not)
Thus, put x = t : y = a(t)3⁄4
=lt(x,y)→(0,0)=ltt→0a9.t274.t−234t+a43.t11
=ltt→0tt×a91+a43
=ltt→0a91+a43
By putting different values of a we get different limits
Thus, there are many paths that do not go to the same place.
Hence, They will not meet every time is the right answer.
a) 1
b) 0
c) ∞
d) Does Not Exist
Answer: d
Explanation: Put x = t : y = a1 * t3⁄4 : z = a2 * t3⁄4
lt(x,y,z)→(0,0,0)(a1)2.t32.(a2)2.t32t3+t2.t.(a1)43+t2.t.(a2)43
lt(x,y,z)→(0,0,0)t3t3×(a1)2.(a2)21+(a1)43+(a2)43
lt(x,y,z)→(0,0,0)(a1)2.(a2)21+(a1)43+(a2)43
By varying a1 : a2 one can get different limit values.
Q 3. Find lt(x,y,z)→(0,0,0)sin(x).sin(y)x.z
a) ∞
b) 1⁄3
c) 1
d) Does Not Exist
Answer: d
Explanation: Put x = t : y = at : z = t
=ltt→0sin(t).sin(at)t2
=ltt→0sin(t)t×(a)×ltt→0sin(at)at
= (1) * (a) * (1) = a
a) ∞
b) 123
c) 9098
d) 8
Answer: d
Explanation: Simplifying the expression yields
lt(x,y,z)→(0,0,0)(x+y)2−z2(x+y)−z
lt(x,y,z)→(0,0,0)(x+y+z).(x+y−z)(x+y−z)
lt(x,y,z)→(0,0,0)(x+y+z)=2+2+4
=8
Q 5. Find lt(x,y,z,w)→(0,0,0,0)x−6.y2.(z.w)3x+y2+z−w
a) 1990
b) ∞
c) Does Not Exist
d) 0
Answer: c
Explanation: Put x = t : y = a1.t1⁄2 : z = a2.t : w = a3.t
lt(x,y,z,w)→(0,0,0,0)t−6.t.(a1)2.t6.(a2)3.(a3)3t+t.(a1)2+a2.t−a3.t
lt(x,y,z,w)→(0,0,0,0)tt×(a1)2.(a2)3.(a3)31+(a1)2+a2−a3
lt(x,y,z,w)→(0,0,0,0)(a1)2.(a2)3.(a3)31+(a1)2+a2−a3
By changing the values of a1 : a2 : a3 we get different values of limit.
Hence, Does Not Exist is the right answer.
a) 700
b) 701
c) 699
d) 22
Answer: d
Explanation: Simplifying the expression we have
lt(x,y,z,w)→(3,1,1,11)(x2+y+z)2−(w)2x2+y+z−w
lt(x,y,z,w)→(3,1,1,11)(x2+y+z+w).(x2+y+z−w)x2+y+z−w
lt(x,y,z,w)→(3,1,1,11)(x2+y+z+w)=(32+1+1+11)
=9+1+1+11=22
Q 7. Given that limit exists find lt(x,y,z)→(−2,−2,−2)sin((x+2)(y+5)(z+1))(x+2)(y+7)
a) 1
b) 3⁄5
c) 1⁄2
d) 0
Answer: b
Explanation: Given that limit exists we can parameterize the curve
Put x = t : y = t : z = t
ltt→−2sin((t+2)(t+5)(t+1))(t+2)(t+7)
ltt→−2sin((t+2)(t+5)(t+1))(t+2)(t+5)(t+1)×ltt→−2(t+5)(t+1)(t+7)
(1)×(−2+5)(−2+1)(−2+7)
=(3).(1)(5)=35
Q 8. Given that limit exist find lt(x,y,z)→(−9,−9,−9)tan((x+9)(y+11)(z+7))(x+9)(y+10)
a) 2
b) 1
c) 4
d) 3
Answer: c
Explanation: We can parameterize the curve by
x = y = z = t
ltt→−9tan((t+9)(t+11)(t+7))(t+9)(t+10)
ltt→−9tan((t+9)(t+11)(t+7))(t+9)(t+11)(t+7)×ltt→−9tan((t+11)(t+7))t+10
=(−9+11)(−9+7)(−9+10)=(2)(2)(1)
=4
More Related PDF Download
Maths Topicwise Free PDF >Click Here To Download |
English Topicwise Free PDF >Click Here To Download |
GK/GS/GA Topicwise Free PDF >Click Here To Download |
Reasoning Topicwise Free PDF >Click Here To Download |
Indian Polity Free PDF >Click Here To Download |
History Free PDF > Click Here To Download |
Computer Topicwise Short Tricks >Click Here To Download |
EnvironmentTopicwise Free PDF > Click Here To Download |
UPSC Notes >Click Here To Download |
SSC Notes Download > Click Here To Download |
Most Important Engineering Mathematics Question
Q 9. Given that limit exists find lt(x,y,z)→(−1,−1,−1)tan((x−1)(y−2)(z−3))(x−1)(y−6)(z+7)
a) 1
b) 1⁄2
c) 1⁄7
d) 2⁄7
Answer: d
Explanation: We can parameterize the curve by
x=y=z=t
ltt→−1tan((t−1)(t−2)(t−3))(t−1)(t−6)(t+7)
ltt→−1tan((t−1)(t−2)(t−3))(t−1)(t−2)(t−3)×ltt→−1(t−2)(t−3)(t−6)(t+7)
=(−1−2)(−1−3)(−1−6)(−1+7)=(3)(4)(7)(6)
=1242=27
Q 10. Given that limit exists find lt(x,y,z)→(2,2,2)(ln(1+xy−2x−y+zxz−2x−6z+12+xz−5x−2z+10xy−7y−2x+14(x−2)(y−2)(z−2))
a) ∞
b) 1
c) 0
d) ln(4⁄5)
Answer: a
Explanation: We can parameterize the curve by
x = y = z = t
ltt→2(ln(1+xy−2x−y+zxz−2x−6z+12+xz−5x−2z+10xy−7y−2x+14(x−2)(y−2)(z−2))
=ltt→2(ln(1+t(t−6)+(t−5)(t−7)(t−2)3)
=ltt→2(ln(1+2(t−6)+(2−5)(2−7))(2−2)3)=ln(45)0→∞
Q 11. Given that limit exists lt(x,y,z)→(0,0,0)(cos(π2−x).tan(y).cot(π2−z)sin(x).sin(y).sin(z))
a) 99
b) 0
c) 1
d) 100
view answer
Explanation: Put x = y = z = t
ltt→0(cos(π2−t).tan(y).cot(π2−t)sin(x).sin(y).sin(z))
ltt→0(sin(t))(tan2(t))sin3(t)
=ltt→0tan2(t)sin(t)=ltt→01cos2(t)
=1cos2(0)=11=1
Q 12. Two men on a 3-D surface want to meet each other. The surface is given by f(x,y)=x−6.y7x+y. They make their move horizontally or vertically with the X-Y plane as their reference. It was observed that one man was initially at (200, 400) and the other at (100, 100). Their meet point is decided as (0, 0). Given that they travel in straight lines, will they meet?
a) They will meet
b) They Will not meet
c) They meet with probability 1⁄2
d) Insufficient information
view answer
Explanation: The problem asks us to find the limit of the function f(x, y) along two lines y = x and y = 2x
For the first line (first person)
x = t : y = 2t
=ltt→0x−6.27.t7t+2t=ltt→027t3t
=273
For the second line (Second Person)
x = t = y
=ltt→0t−6.t7t+t=ltt→0t2t
=1/2
The limits are different and they will not meet.
Q 13. Two men on a 3-D surface want to meet each other. The surface is given by f(x,y)=x6.y7x13+y13. They make their move horizontally or vertically with the X-Y plane as their reference. It was observed that one man was initially at (400, 1600) and the other at (897, 897). Their meet point is decided as (0, 0). Given that they travel in straight lines, will they meet?
a) They will meet
b) They will not meet
c) They meet with probability 1⁄2
d) Insufficient information
Explanation: The problem asks us to find the limit of the function f(x, y) along two lines y = x and y = 4x
For the first line (first person)
x = t : y = 4t
=ltt→0t6.47.t7t13+413t13=ltt→047tt(1+413)
=471+413
For the second line (Second Person)
x = t = y
=ltt→0t6.t7t13+t13=ltt→0t132t13
= 1⁄2
The limits are different and the will not meet.
Q 14. Observe the figure. It is given that the function has no limit as (x, y) → (0 ,0) along the paths given in the figure. Then which of the following could be f(x, y)
a) f(x,y)=x7.y8(x+y)
b) f(x,y) = x2y7
c) f(x,y)=xy2(x2+y2)
d) f(x,y)=x6.y2(y5+x10)
Answer: d
Explanation: The curves in the given graph are parabolic and thus they can be parameterized by
x = t : y = at2
Substituting in Option f(x,y)=x6.y2(y5+x10) we get
=ltt→0t6.a2.t4a5.t10+t10
ltt→0t10t10×a2a5+1
ltt→0a2a5+1
By varying a we get different limits
Topic Related PDF Download
pdfdownload.in will bring you new PDFs on Daily Bases, which will be updated in all ways and uploaded on the website, which will prove to be very important for you to prepare for all your upcoming competitive exams.
The above PDF is only provided to you by PDFdownload.in, we are not the creator of the PDF, if you like the PDF or if you have any kind of doubt, suggestion, or question about the same, please send us on your mail. Do not hesitate to contact me. [email protected] or you can send suggestions in the comment box below.
Please Support By Joining Below Groups And Like Our Pages We Will be very thankful to you.
- Facebook Page: https://www.facebook.com/onlyupsc/
TEGS:-engineering mathematics 1 matrices notes pdf,engineering mathematics 2 handwritten notes,1st year pre engineering maths notes,engineering mathematics notes made easy,engineering mathematics 1 handwritten notes,gate mathematics notes pdf,gate mathematics notes made easy pdf,engineering m1 notes pdf